Using computer simulation to generate sequence data for protein families,
we studied the influence of among site rate variation on the performance
of phylogenetic reconstruction. The following methods for phylogenetic
reconstruction were compared: maximum likelihood, parsimony, and distance-matrix
analyses. Three different tree topologies were used to explore the effect
of long branch attraction with data that incorporated substitution bias
and different degrees of among site rate variation.
While all methods showed errors due to long branch attraction under
extreme conditions, maximum likelihood was by far the most successful in
accurately resolving deep phylogenies.
Using protein parsimony long branch attraction already became a problem
with modest differences in rate (ratio 1:3) and sequences that were about
50% identical, where as maximum likelihood methods still performed well
with realistic values of among site rate variation and branch length ratios
of 1:12 (sequences less than 30% identical).
In the absence of fast evolving lineages (i.e., long branches were due
to the absence of side branches only) all tested algorithms performed well
even when sequences were below 20% identity.
INTRODUCTION
Systematic artifacts have long been recognized as important
complications in phylogenetic reconstruction. The most serious of this
is long branch attraction (e.g.: Felsenstein, 1978, Handy and Penny, 1989).
Long branch attraction occurs when a phylogeny is being reconstructed that
contains long branches that group intermingled with shorter branches. Two
scenarios can yield long branches:
- some sequences evolve faster than others, i.e., they experience faster
substitution rates. (Tree Type #1)
- the long branches can be due to the absence of side branches in some
lineages (Tree Type #3)
In both instances most algorithms tend to group the long
branches together regardless whether this grouping reflects the actual
history. Once the length of the long branches is above a threshold, which
is different for different algorithms, the wrong result, i.e. grouping
the long branches together, is produced with high reproducibility (compare
Fig. 2). In case of parsimony analysis this finding can be rephrased in
the statement that the actual evolution is not necessarily most parsimonious.
Protein sequences are useful for comparisons between distantly
related sequences because their 20 letter alphabet in conjunction with
substitution bias facilitates the alignment of divergent sequences (Pearson,
1996). Sequence alignment is further aided by highly conserved residues
that remain unchanged even between distantly related proteins.
In case of nucleotide sequences simulations have been
performed to estimate the effect of among site rate variation (ASRV) on
phylogenetic inference (e.g.: Kuhner and Felsenstein, 1994, Huelsenbeck,
1995, Tateno et al, 1994); however at present the effect of ASRV on long
branch attraction on protein sequences based phylogenies has not been explored.
In this study we simulate protein data for different tree topologies using
four different distributions for ASRV.
MATERIALS AND METHODS
Three different tree topologies were considered. For each
topology independent data sets were generated by simulating substitution
events. Among site rate variation and substitution bias were taken into
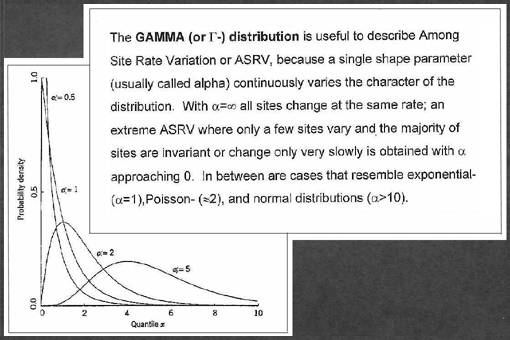
account. Different degrees of among site rate variation can be described
using different shape parameters for the Gamma distribution. Four values
of shape parameters were used: infinity (no ASRV), 0.98 (exponential distribution),
0.66 and 0.5 were used. Values of 0.98 and 0.66 for a were chosen
because they represent values estimated for a variety of different protein
families (Gogarten et al., 1996). The value of 0.5 for a was chosen
because of indications that substitution patterns in extreme thermophiles
follow a more extreme site to site variation (Liu et al. submitted).
For each value of shape parameter data sets with different
branch lengths were generated. The distribution of the different rate classes
along the sequence was chosen to mimic the spatial distribution observed
in vacuolar and archaeal ATPase A-subunits (Gogarten et al., 1992).
The observed frequency of residues falling into each rate
category was used to discretize a continuous Gamma distribution. Lower
and upper bounds for each rate category were calculated so that the portion
of the gamma distribution falling within these bounds corresponded to the
observed frequency of that rate category. The rate assigned to each category
was determined from of the median of the gamma distribution within the
corresponding lower and upper bounds.
We used several programs for analyzing the simulated data:
PUZZLE 3.0 (Strimmer and van Haeseler, 1996) for maximum likelihood, PHYLIP
3.5 package (Felsenstein, 1993) and PHYLOWIN (Galtier et al 1996) for parsimony,
neighbor joining and Fitch-Margoliash (Fitch and Margoliash, 1967) methods,
CLUSTALW 1.6 (Thompson et al., 1994) for neighbor joining method with prior
alignment of the data.
THE SIMULATION ALGORITHM
Fig.1: Schematic diagram of the algorithm
used to simulate protein sequence evolution.
The algorithm was developed by Lei Liu et al. to study
the relationship between genetic distance and % sequence divergence in
the presence of different degrees of Among Site Rate Variation. The algorithm
uses a discrete approximation to a continuous Gamma distribution to describe
ASRV (Yang, 1996b).
The distribution of rate classes along the sequence (i.e.
the correlation between sites) was chosen to mimic the distribution found
in ATPase catalytic subunits. This is necessary because slower evolving
sites are not randomly distributed along the sequence, but clustered together.
The frequency of the rate classes was chosen to approximate a continuous
distribution. The resulting algorithm thus provides sequences with realistic
ASRV, substitution bias and correlation between sites. The algorithm is
consistent with estimation of ASRV through the maximum likelihood programs
PUZZLE(Strimmer and van Haeseler, 1996) and PAML (Yang, 1996).
THE TREE TYPES
 |
Tree type#1 tests for long branch attraction due to different
substitution rates in different lines of descent. |
 |
Tree type#2 tests for "long branch repulsion".
An algorithm could do well on type#1 trees not because it is better in
extracting phylogenetic information, but because it has the tendency to
group long branches apart from each other. In the latter case, this algorithm
should do poorly on type#2 trees. |
 |
Tree type#3 tests for long branch attraction in the absence
of fast evolving lineages. The tree conforms to a molecular clock, the
long branches are due only to the absence of side branches. |
RESULTS AND DISCUSSION
All of the tested algorithms are susceptible to long branch
attraction. In the absence of ASRV errors due to long branch attraction
only occur with sequences that show less than 20% identity (Tab. 1); however,
in the presence of ASRV long branch attraction becomes a serious problem
even when the sequences at the "long" branches are about 50%
identical. Use of maximum likelihood methods that incorporate both substitution
bias and ASRV is superior over parsimony analysis. However, even this approach
falls victim to long branch attraction with more extreme ASRV (a =
0.5 and 0.66).
Test of algorithms for errors due
to long branch attraction.
Sequence simulations used the indicated values
for shape parameters and branch lengths. '+' denotes that the tree topology
was correctly recovered, '-' indicates that the wrong tree was recovered
(i.e., the long branches A and B grouped together). 'n/a' denotes that
data could not be analyzed with the method. Signs n the brackets indicate
that the result was found in two out of three replicates.
Fig. 2: Correlation between branch length
and average of bootstrap probability calculated with clustalw (with alignment,
gaps excluded, no correction for multiple hits). the white column denotes
correct, the black columns the incorrect tree. Bars indicate standard deviations
calculated from independent simulations.
Table 2 shows that none of the tested algorithm makes
the opposite error (i.e., long branch repulsion). The better performance
of some algorithms indeed appears to be due to the better extraction of
phylogenetic information by these algorithms.
Test of algorithms for long branch
repulsion.
For further explanations see text
and table 1.
The better performance of the used maximum likelihood
approaches is also indicated in the results of Table 3. However, all of
the algorithms performed surprisingly well, when the long branches were
not due to unequal substitution rates but due to the absence of side branches.
Even when the sequences were aligned prior to phylogenetic reconstruction,
phylogenies were accurately recovered when sequences were less than 20%
identical. (No one in his right mind would sequences which are less than
10% identical for phylogenetic information).
Test for long branch attraction due
to missing side branches only.
'+' denotes that the tree topology was correctly
recovered, '-' indicates that the wrong tree was recovered (i.e., the long
branches A and B grouped together). 'n/a' denotes that data could not be
analyzed with the method and 'u' indicates that the tree was unresolved.
Signs n the brackets indicate that the result was found in two out of three
replicates.
If genetic distances used as the basis for comparison,
ASRV facilitates phylogenetic reconstruction (Tab.3), especially if the
alignment step is included.
CONCLUSION
Avoid
data sets that contain fast and slow evolving sequences.
If data
sets contain long branches that are due to higher substitution rates, maximum
likelihood analyses that incorporate ASRV and substitution bias perform
better than protein parsimony of distance matrix analyses.
Long
branch attraction that is due to the absence of side branches does not
appear to be a serious problem for phylogenetic reconstruction from amino
acid sequences.
ACKNOWLEDGMENTS
Work in this project was supported through the NASA
Exobiology Program. While working on this project Olga Zhaxybayeva
was supported through the NASA Planetary Biology
Internship Program. We thank Lei Liu
and Kent Holsinger for stimulating
discussions and suggestions, and Lei Liu for providing the algorithm used
to simulate sequence evolution.
REFERENCES
- Felsenstein, J. (1978) Cases in which parsimony and
compatibility methods will be positively misleading. Syst. Zool. 27,
401-410
- Felsenstein, J. (1993) Phylogeny Inference Package,
version 3.5c. Distributed by the author. Dept. of Genetics, Univ. of Washington,
Seattle.
- Fitch, W. M., and E. Margoliash (1967). Construction
of phylogenetic trees. Science 155: 279-284
- Galtier, N., Gouy, M., and Gautier, C. (1996). SEAVIEW
and PHYLO_WIN: two graphic tools for sequence alignment and molecular phylogeny.
CABIOS 12: 543-548
- Gogarten, J.P., L. Olendzenski, E. Hilario, C. Simon,
and K.E. Holzinger (1996). Dating the cenancestor of organisms, Science
274: 1750-1751.
- Gogarten, J.P., T. Starke, H. Kibak, J. Fichmann,
and L. Taiz (1992). Evolution and Isoforms of V-ATPase Subunits. The Journal
of Experimental Biology 172: 137-147
- Hendy, M.D., Penny, D. (1989) A framework for the
quantitative study of evolutionary trees. Syst. Zool. 38, 297-309
- Huelsenbeck, P.J. (1995) Performance of phylogenetic
methods in simulation. Syst. Biol. 44, 17-48.
- Pearson, W.R. (1996) Effective protein sequence comparison.
Meth. Enzymol. 266, 227-258.
- Strimmer K., and A, von Haeseler 1996. Quartet puzzling:
a quartet maximum likelihood method for reconstructing tree topologies.
Mol Biol Evol 13, 964-969.
- Tateno, Y., Takezaki, N., Nei, M. (1994) Relative
efficiencies of the maximum likelihood, neighbor-joining, and maximum-parsimony
methods when substitution rate varies with site. Mol. Biol. Evol. 11,
261-277.
- Thompson, J.D., Higgins, D.G. and Gibson, T.J. (1994)
CLUSTAL W: improving the sensitivity of progressive multiple sequence alignment
through sequence weighting, positions-specific gap penalties and weight
matrix choice. Nucleic Acids Research, 22:4673-4680.
- Yang, Z. (1996) Phylogenetic analysis by maximum
likelihood (PAML), Version 1.2. Department of Integrative Biology, UCBerkeley,
CA
- Yang, Z. (1996b) The among-site rate variation and
its impact on phylogenetic analyses, Trends Ecol.Evol. 11, 367-372